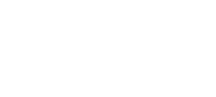Code & CI/CD, built for teams using Jira
With best-in-class Jira integration, and built-in CI/CD, Bitbucket Cloud connects developer workflows from planning to incident management. Join millions of developers who choose to build on Bitbucket.
Migrating to cloud? Listen to this webinar on Bitbucket Cloud's enterprise strategy + get migration tips.
PRODUCT FEATURES
Why choose Bitbucket Cloud?
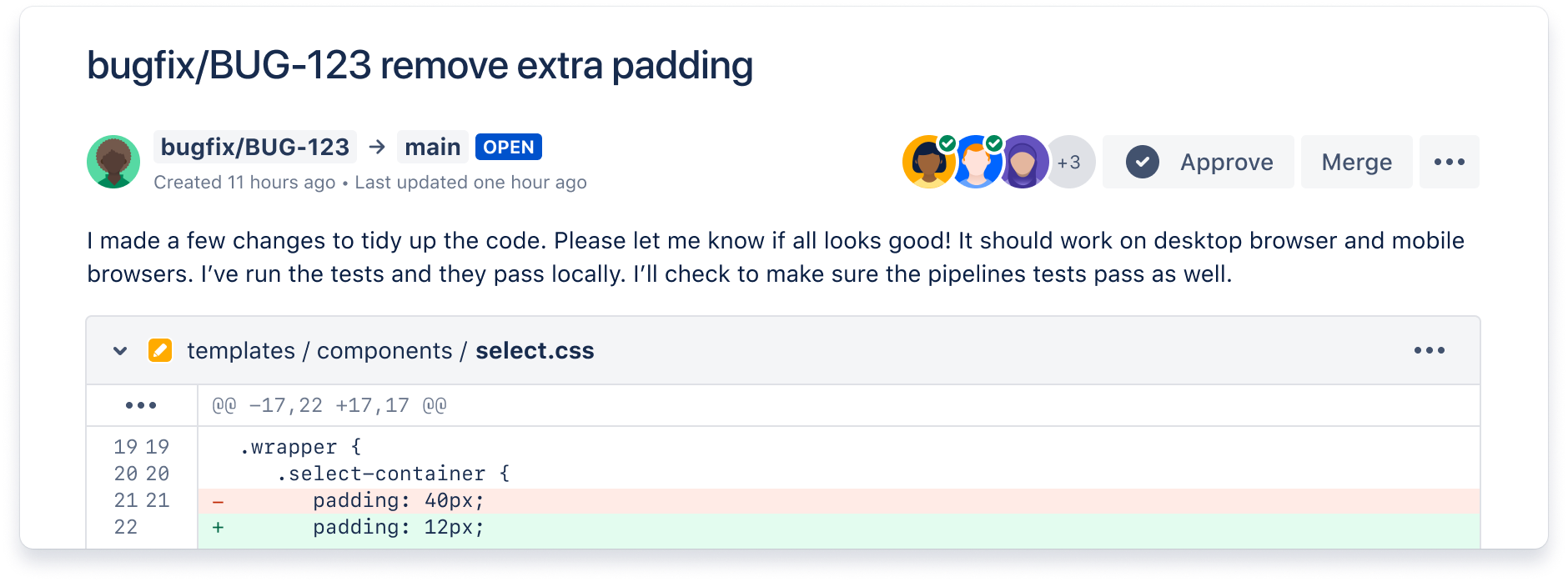
Collaborate across multiple teams
Reduce context-switching by managing your Jira issues in Bitbucket with the built-in Jira UI. And when you include your issue key in commits, your Jira issue statuses update automatically.
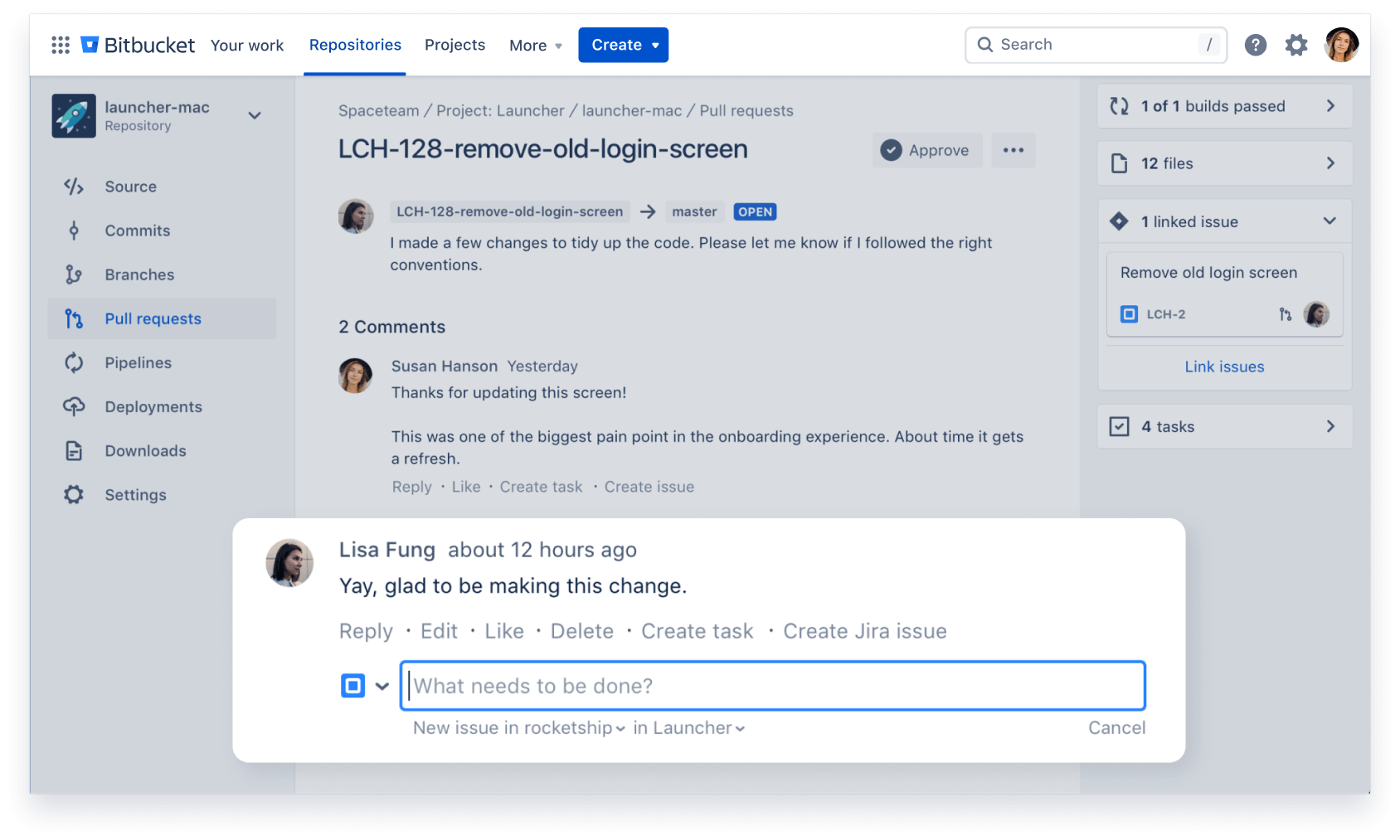
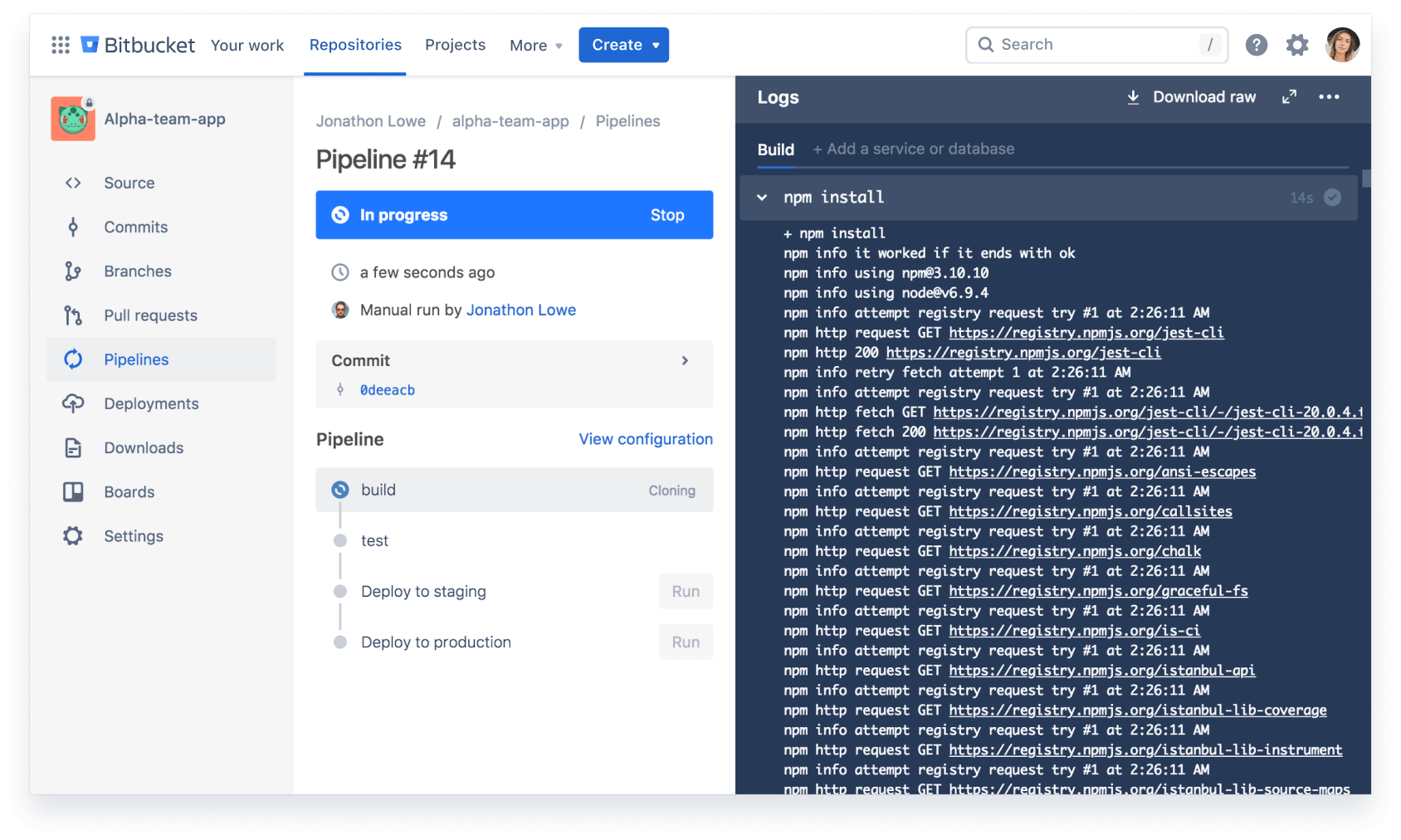
Ship quality code
Comprehensive code review features to help you find and fix bugs before you deploy. Review large diffs with ease, view third-party code reports, and open Jira tickets right from the PR screen.
Automate deployments
Use our built-in CI/CD tool, Bitbucket Pipelines, to create powerful, automated workflows. Or connect Bitbucket Cloud to on-prem CI/CD tools like Bamboo or Jenkins.
watch THE demo
See how Bitbucket Cloud works with Atlassian tools
This video demos a code change workflow using Jira Software and Bitbucket Pipelines.
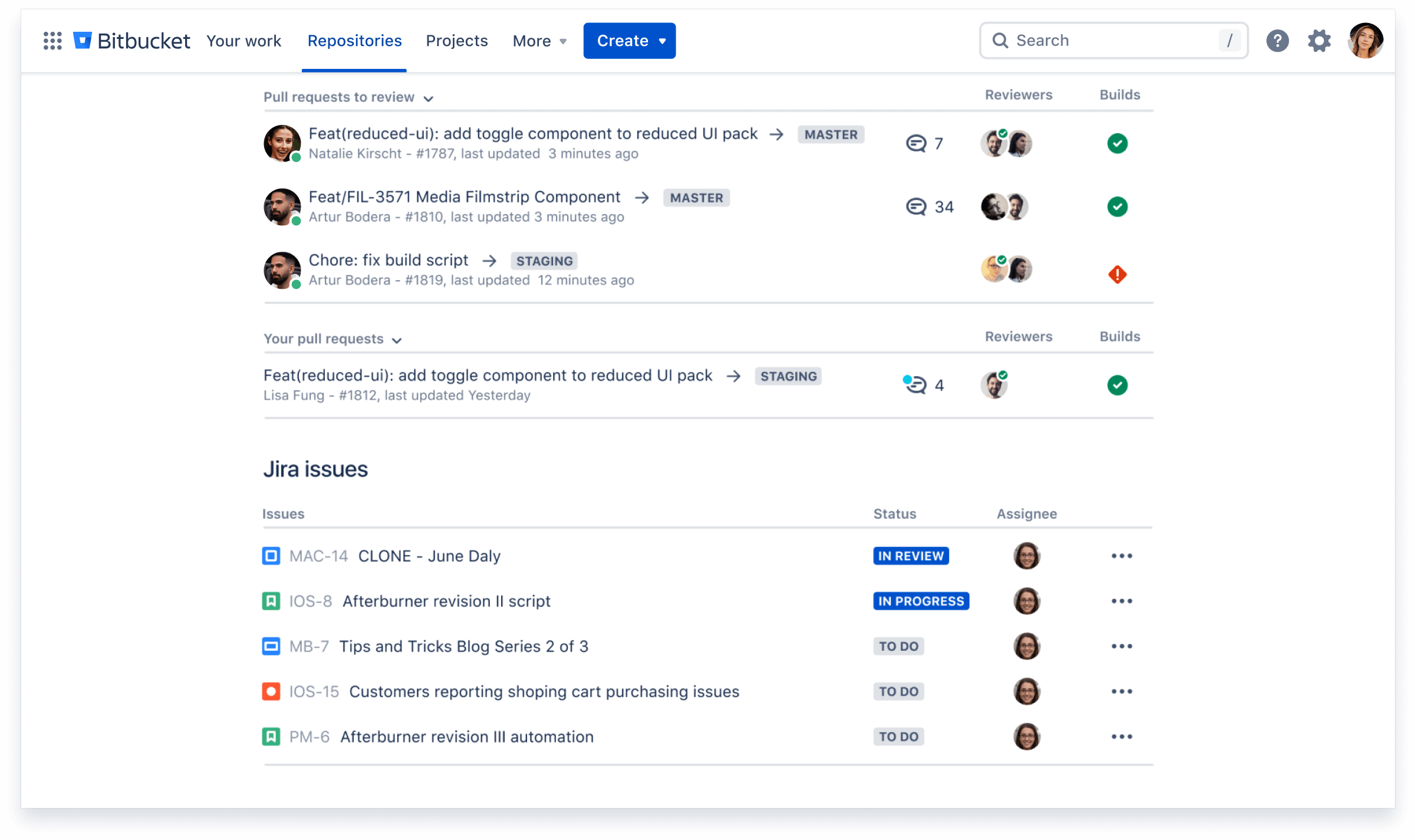
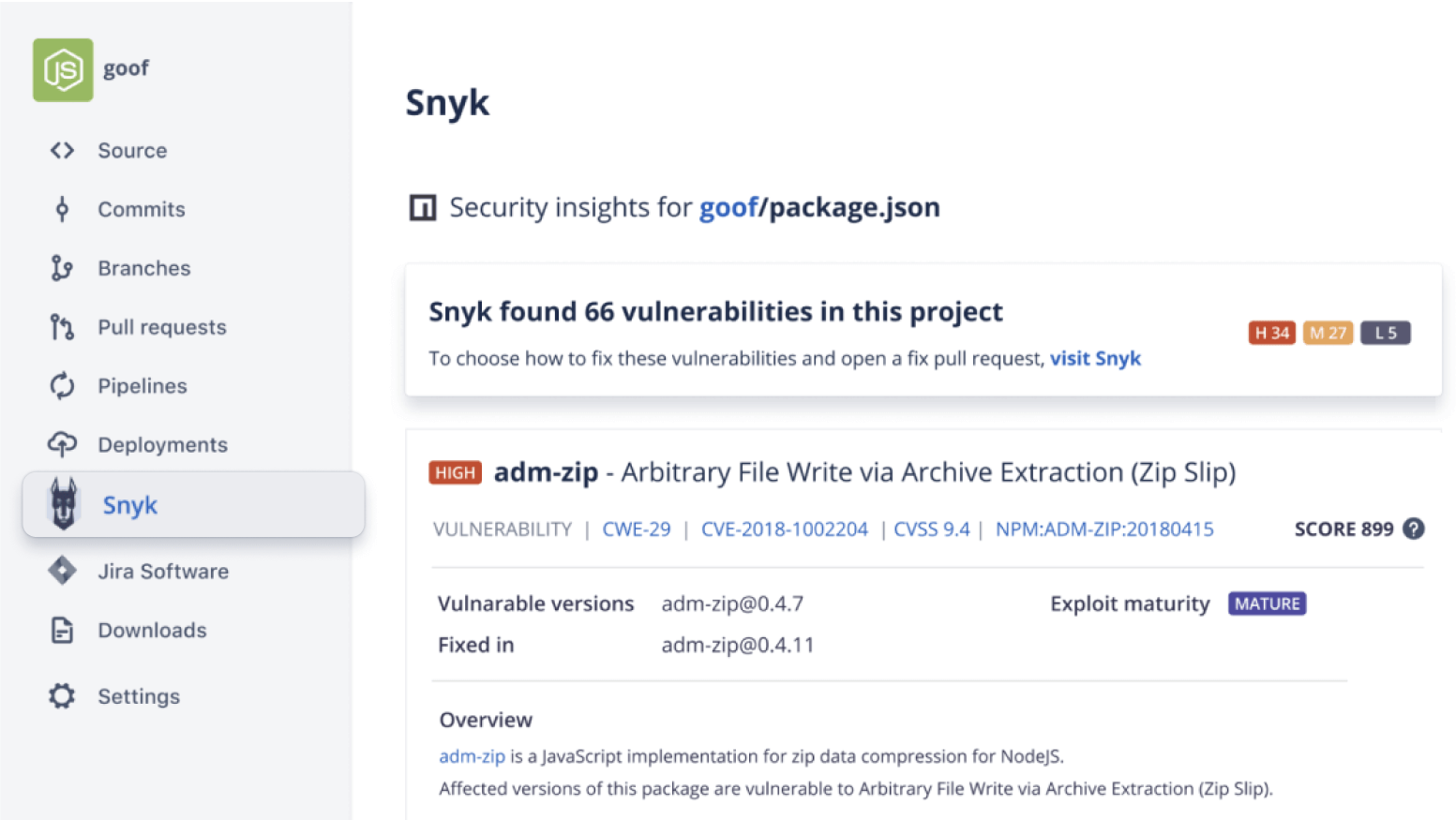
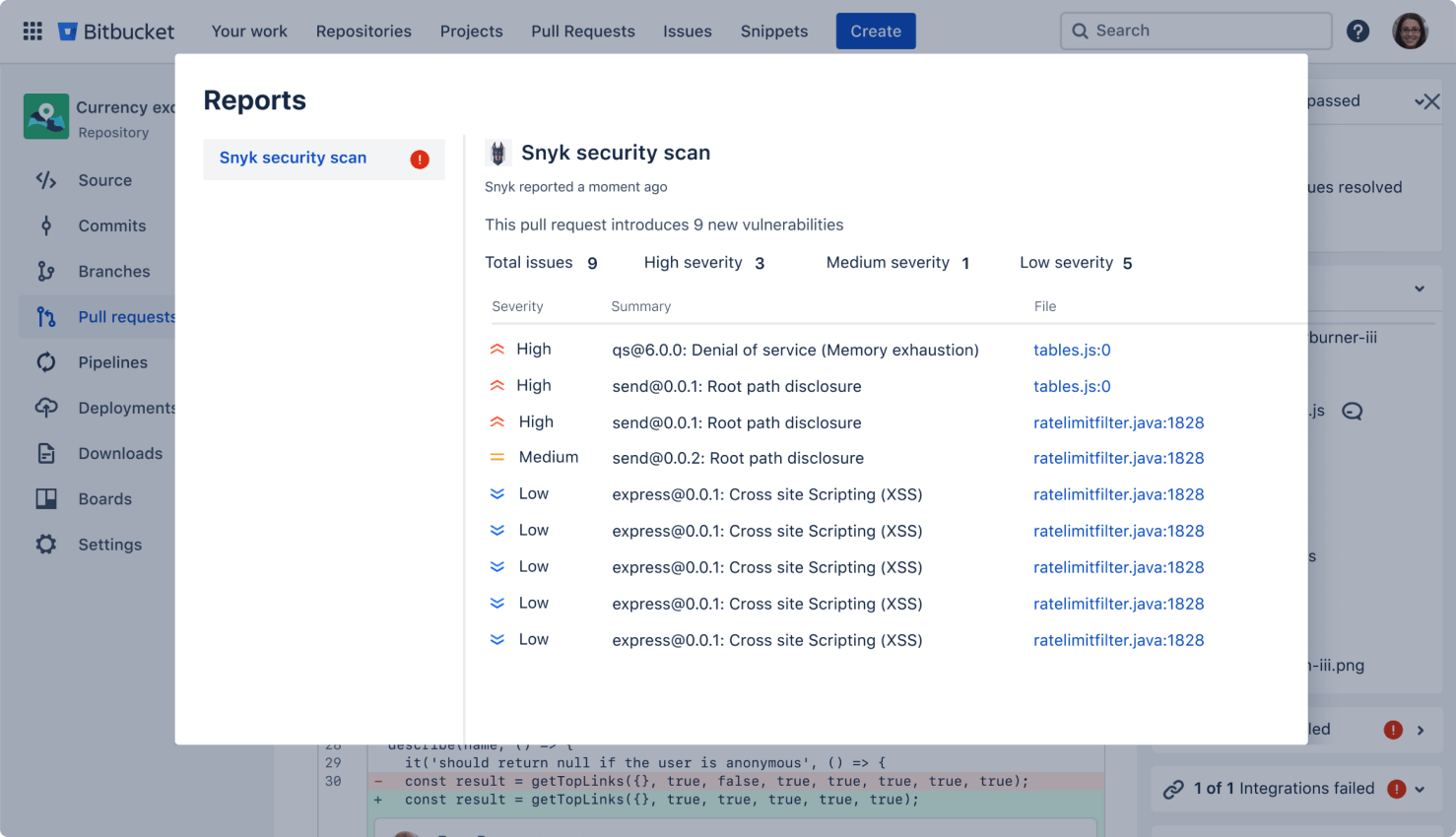
Secure your code
Run automatic security scans with out-of-the-box integration with Snyk, or connect to other providers. Simply open an existing repository or create a new one and navigate to the Security tab to install the Snyk integration.
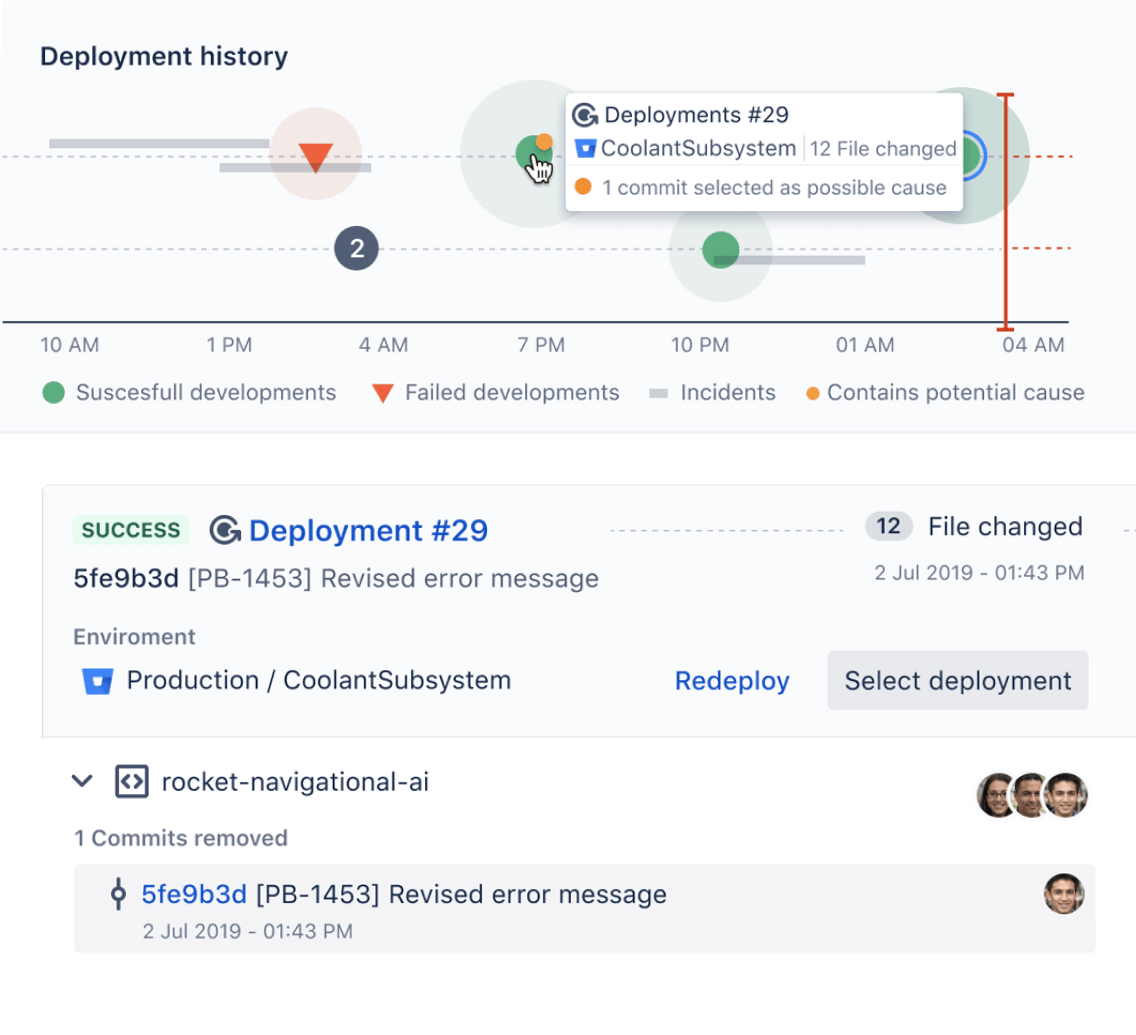
Collaborate with IT Ops
Enable automated change approval processes and resolve incidents faster by mapping incidents to deployments with Bitbucket and Jira Service Management. Learn more

Secure & compliant
Bitbucket Cloud is compliant with SOC2/3, ISO, and GDPR. 2FA and IP allowlisting keep your code accessible only by authorized users. All code is encrypted in transit and at rest.








Integrations for every team
Build a DevOps toolchain that works for you
Don’t settle for an all-in-one DevOps tool. Start by connecting Bitbucket and Jira Software via Atlassian’s Open DevOps solution, then build out your custom DevOps stack with market-leading partner tools across security, testing and monitoring.
15 million developers from over a million teams love Bitbucket
Learn more

Need a self-hosted option?
Bitbucket Data Center is our code collaboration tool built for teams who need to host code behind the firewall.

Considering migrating to Bitbucket Cloud?
Our free migration app automates moving your code and users from Bitbucket Server or Data Center to Bitbucket Cloud.

New features on the horizon
Learn more about what we’ve recently shipped and what we’re building next for your team.
Take Bitbucket Cloud for a spin
Built for professional teams
Bitbucket is more than just Git code management. Bitbucket gives teams one place to plan projects, collaborate on code, test, and deploy.
If you're looking for our self-managed option, check out

Free unlimited private repositories
Free for small teams under 5 and priced to scale with Standard ($3/user/mo) or Premium ($6/user/mo) plans.

Bitbucket for DevOps
Bitbucket integrates with first- and third-party tools to reduce context-switching and improve code quality. Learn more about using Bitbucket for DevOps.

Built-in Continuous Delivery
Build, test and deploy with integrated CI/CD. Benefit from configuration as code and fast feedback loops.
Devsecops
Build secure software from the start
Bring security directly into every stage of the development process. Get real-time visibility into any security issues in their code and containers, identify vulnerability fixes early in development and monitor new risks post deployment.
New to Git?
No problem. We have resources to get you up to speed, quickly.

Learn Git with interactive tutorials
Make Bitbucket your Git sandbox with tutorials that bring you up to speed with Git and help you build effective workflows.
Download Sourcetree, our free Git GUI.
Say goodbye to the command line - Sourcetree simplifies how you interact with your Git repositories so you can focus on coding.
Simple plans hosted in the cloud. Priced to scale.
Free
Standard
Premium
101+ users? We offer discounts for large teams! Calculate your price